Der letzte Blog-Beitrag befasste sich mit Gott und der Berliner Mauer. Gemeint war nicht der Allmächtige, sondern der Wissenschaftler Richard J. Gott. Heute ist es umgekehrt. Heute geht es um einen mathematischen Beweis für die Existenz Gottes. Der Physiker Heinz Oberhummer sagt, das sei nicht möglich. Der Mathematiker Kurt Gödel sah das anders.
Gödel (1906 – 1978) war ein legendärer Logiker. Wie Einstein lehrte er an der Universität Princeton, die beiden großen Männer waren befreundet. Einstein sagte einmal, dass er manchmal nur deshalb ins Institut gegangen sei, um später mit Gödel auf dessen Heimweg sprechen zu können.
Es gibt Wahrheiten, die sich nicht beweisen lassen
Nach Gödels Tod tauchte in seinem Nachlass ein mathematischer Beweis für die Existenz Gottes auf. Gödel hatte ihn nicht veröffentlicht, weil er besorgt war, man könne ihn als Glaubensbekenntnis auffassen. Der Fund im Nachlass war eine wissenschaftshistorische Sensation. Schon zu Lebzeiten wurde Gödel berühmt durch seinen Unvollständigkeitssatz. Er stieß darauf, als er sich mit Aussagen vom Typ „Ich bin nicht beweisbar!“ befasste und die Frage nach ihrem Wahrheitsgehalt stellte.
Ist diese Aussage wahr, dann kann man sie – wie sie ja selbst verkündet – nicht beweisen. Ist diese Aussage falsch, schon. Doch tut man dies, so hat man etwas bewiesen, das nicht wahr ist. Das ist ein logischer Widerspruch. Ergo ist die getroffene Aussage nur dann wahr, wenn sie nicht bewiesen werden kann. Es gibt also Wahrheiten, die sich nicht beweisen lassen. Das ist der Kern von Gödels Unvollständigkeitssatz. Und damit hatte er die Mathematik in ernste Schwierigkeiten gebracht.
Irgendwann muss Gödel begonnen haben, logisch über Gott nachzudenken. Der Ausgangspunkt seines Gottesbeweises ist der Leibnizsche Begriff der positiven Eigenschaft. Eine Eigenschaft ist positiv, wenn sie keiner anderen Eigenschaft logisch widerspricht. Ferner spielt der Begriff der Notwendigkeit eine Rolle: Notwendig ist etwas, dessen Gegenteil logisch widersprüchlich ist.
Drei Definitionen, fünf Axiomen und vier Theoreme
Gödels logische Konstruktion Gottes besteht aus drei Definitionen, fünf Axiomen und vier Theoremen. Gleich in der ersten Definition teilt er uns mit, wie er sich Gott denkt. Definitionen sind Begriffsfestlegungen, Axiome sind die Voraussetzungen des Beweisganges, die ohne Begründung als wahr angenommen werden. Theoreme sind aufgrund der Axiome und mittels gültiger logischer Schlüsse erhaltene wahre Aussagen.
Hier ist Gödels Beweis in versprachlichter Form. Haben Sie Lust, ihn nachzuvollziehen?
Definition 1: Ein Wesen ist göttlich, wenn es alle positiven Eigenschaften besitzt.
Definition 2: Eine Eigenschaft eines Wesens heißt wesentlich, wenn alle weiteren Eigenschaften dieses Wesens daraus notwendig folgen.
Definition 3: Ein Wesen existiert notwendig, wenn alle seine wesentlichen Eigenschaften notwendig sind.
Axiom 1: Jede Eigenschaft ist entweder positiv oder nicht positiv.
Axiom 2: Was notwendig eine positive Eigenschaft enthält, ist selber positiv.
Theorem 1: Ist eine Eigenschaft positiv, so ist es möglich, dass es etwas gibt, das diese Eigenschaft besitzt.
Axiom 3: Göttlichkeit ist eine positive Eigenschaft.
Theorem 2: In einer möglichen Welt ist ein göttliches Wesen logisch möglich.
Axiom 4: Jede positive Eigenschaft ist notwendig positiv.
(Dies bedeutet, dass Notwendigkeit in der Positivität einer Eigenschaft enthalten ist. Somit ist Notwendigkeit selbst eine positive Eigenschaft.)
Theorem 3: Wenn ein Wesen göttlich ist, dann ist seine Göttlichkeit eine wesentliche Eigenschaft.
(Daraus folgt, dass es höchstens ein göttliches Wesen geben kann.)
Axiom 5: Die Eigenschaft der notwendigen Existenz ist positiv.
Theorem 4: Wenn die Existenz eines göttlichen Wesens logisch möglich ist, dann ist sie notwendig.
(Da wir die logische Möglichkeit der Göttlichkeit bereits in Theorem 2 festgestellt haben, folgt nun, dass genau ein göttliches Wesen notwendig existiert.)
Der Beweis ist logisch korrekt, wie jetzt ein Computer mithilfe zweier Informatiker geprüft hat.
Bei Gödel sieht der Beweis in abstrakter Form so aus. Gödels Gott ist am Ende das G(x):
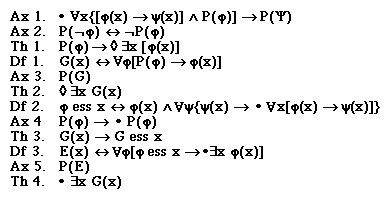
Was halten Sie von diesem Beweis? Glauben Sie an G(x)? Was halten Sie von Gödels Gott? Für mich ist eins klar: Den „Gott Abrahams, Isaaks und Jakobs“ aus meinem Religionsunterricht habe ich anders in Erinnerung.