Nach den tiefer schürfenden Beiträgen der letzten Wochen kommt heute etwas zur Entspannung. Kürzlich las ich ein Werbeplakat mit der Aufschrift „Mach was gegen hässlich„. Das kann natürlich jeder nur in seinem Bereich tun. Und da mein Bereich eben nun mal größtenteils die Mathematik ist, versuche ich etwas gegen hässliche Mathematik zu tun.
Verschönern wir also die Mathematik. Die von vielen als emotional karg empfundene Disziplin könnte in neuer Darreichungsform möglicherweise ihre Fangemeinde erheblich vergrößern. Einen Versuch ist es jedenfalls wert.
Ich werde, was ich meine, an einem Beispiel verdeutlichen: Nehmen wir uns eines der grundlegendsten logischen Denkgesetze vor, den Umkehrschluss. Das ist der logische Schluss von „Aus P folgt Q“ auf „Aus nicht Q folgt nicht P“. Also zum Beispiel: „Wenn heute Donnerstag ist, dann ist morgen Freitag“ impliziert „Wenn morgen nicht Freitag ist, dann ist heute nicht Donnerstag.“
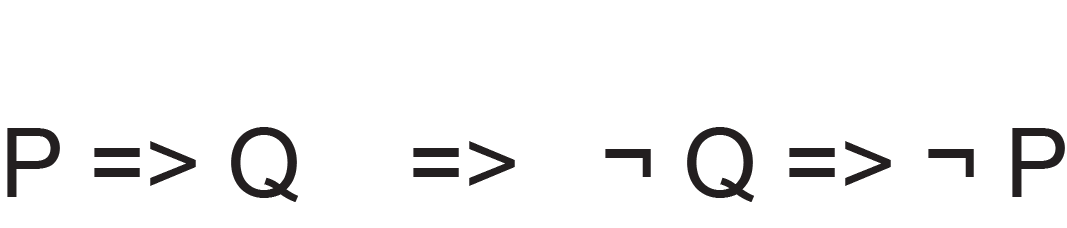
Mathematiker machen daraus die zwar kompakte, aber unter ästhetischen Gesichtspunkten keinen Lustgewinn liefernde Formel:
Ich kann dieses Denkgesetz natürlich auch auf Zitate, Sprüche und Sprichwörter anwenden: „Wenn einer eine Reise tut, dann kann er was erzählen“, sagte schon Matthias Claudius 1786 in Urians Reise um die Welt. Oder mit dem Umkehrschluss zwar logisch äquivalent, aber weniger poetisch: „Wenn einer nichts zu erzählen hat, dann ist er nicht gereist.“
Der Vorteil der Mathematik besteht darin, dass ihre Wahrheiten trotz Änderung der Bezeichnungsweisen erhalten bleiben. Nichts hindert also, den mathematischen Formalismus visuell aufzumöbeln.
In der mathematischen Logik spielen die Operationen Negation („nicht“), Konjunktion („und“), Disjunktion („oder“), Implikation („wenn, dann“), Äquivalenz („dann und nur dann“) eine wichtige Rolle. Warum also nicht dafür einige hübsche Piktogramme einführen, entsprechend obiger Reihenfolge
Und als Trennungszeichen nehmen wir:
Ferner benötigen wir noch Symbole, die Aussagen darstellen:
Und flugs wird aus der obigen kargen Mitteilung des Umkehrschlusses bei (*) ein visuell erstklassiges Statement:
(Abbildungen von Vlad Sasu)
Das Bild ist unverändert randvoll mit Wahrheitsgehalt, hat aber darstellungsästhetisch mindestens so viel dynamischen Sex-Appeal wie ein Schwingdeckelmülleimer. Versuch gescheitert! Oder?