In Sotschi findet derzeit der Schachweltmeisterschaftskampf zwischen Magnus Carlsen und Viswanathan Anand statt. Klar, dass wir vom Schach deshalb auch im Mathe-Blog Notiz nehmen. Was das Bindeglied zwischen Mathematik und Schach ist? Die Logik.
„Die Logik ist die Hygiene, deren sich der Mathematiker bedient, um seine Gedanken gesund und kräftig zu erhalten“, sagte einst der Mathematiker Hermann Weyl. Und schon früher adelte Gottfried Wilhelm Leibniz das Schachspiel mit der Bemerkung: „Die erstaunliche Logik und die mathematische Exaktheit stellen das Schachspiel auf eine Stufe mit jeder exakten Wissenschaft.“ Das sind gewichtige Worte von ernstzunehmenden Denkern. Aber Logik, was ist das eigentlich?
Logik befasst sich mit den Prinzipien des schlüssigen Denkens und Beweisen. Sehen wir uns ein Alltagsbeispiel an: Drei Mathematiker sitzen im Café. Kommt die Bedienung und sagt: „Möchten Sie alle etwas trinken?“ Sagt der erste Mathematiker: „Ich weiß nicht.“ Sagt der zweite Mathematiker: „Ich weiß nicht.“ Sagt der dritte Mathematiker: „Nein.“ Wie ist dieser Dialog zu verstehen? Man muss nur ein wenig vor- und zurückschreitende Logik einsetzen.
Hinter der stenografisch kurzen Antwort steckt eine ganze Geschichte
Die Bedienung hatte gefragt, ob alle etwas trinken möchten. Mit seiner stenografisch kurzen Antwort teilt der erste Mathematiker uns Folgendes mit: „Also ich möchte ein Getränk, aber ich weiß nicht, wie es bei den anderen beiden ist, und zum jetzigen Zeitpunkt ist somit noch ein Ja oder ein Nein als Antwort auf die Frage möglich.“ Wenn der erste Mathematiker nichts hätte trinken wollen, dann hätte er die Frage definitiv schon mit Nein beantworten können.
Nun kommt der zwei Mathematiker. Aus der Antwort des ersten Mathematikers hat er geschlossen, dass dieser etwas trinken möchte. Der Antwort des zweiten Mathematikers können wir entnehmen: Auch er möchte etwas trinken (andernfalls hätte auch er mit Nein antworten müssen) und er weiß zwar, dass auch Mathematiker 1 etwas trinken möchte, weiß aber nicht, wie es sich mit Mathematiker 3 verhält. Insofern kann auch er noch kein definitives Ja oder Nein geben.
Nun kommt der dritte Mathematiker. Er hat aus den Antworten seiner Vorgänger entnommen, dass sie etwas trinken wollen. Er aber möchte nichts trinken. Deshalb kann er ein klares Nein als Antwort auf die Frage der Bedienung geben.
Rückschreitende Logik am Beispiel erklärt
Nach diesem Vorspiel sind wir bereit für ein faszinierendes Schachrätsel, das sich mit rückschreitender Logik lösen lässt. Betrachten Sie dafür das folgende Schachbrett:
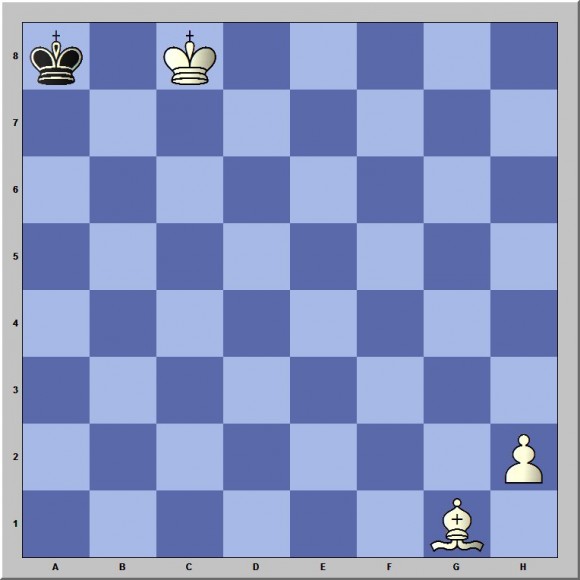
Die Frage lautet: Kann Schwarz soeben einen legalen Zug gemacht haben? Und wenn ja, welche Züge müssen vor der Brettstellung geschehen sein? Es geht also darum, in die Vergangenheit zu schauen. Das erfordert logische Detektivarbeit. Eines ist klar: Wenn Schwarz überhaupt ziehen konnte, dann hat er zuletzt mit seinem König gezogen. Und zwar nach a8. Aber das ist mir noch ein bisschen zu vage. Wir wollen ja das, was in der jüngsten Vergangenheit vor der Brettstellung passiert ist, auch verstehen. Wie kann denn der schwarze König überhaupt nach a8 gezogen sein?
Wegen der Position des weißen Königs kann der schwarze König nur von a7 nach a8 gelangt sein. Doch auch, dass er von a7 kam, scheint wegen des weißen Läufers auf g1 eigentlich unmöglich. Es ist aber die einzige theoretische Möglichkeit für das der Stellung vorausgehende Standfeld des schwarzen Königs. Wir müssen deshalb überlegen, ob wir Begleitumstände finden können, die dies ermöglichen.
Und in der Tat: Der schwarze Monarch kann von a7 gekommen sein, wenn eine Figur auf b6 stand, die verhindert hat, dass er dort im Schach stand. In der obigen Stellung ist diese Figur nicht mehr auf dem Brett. Sie muss demnach, seit sie den schwarzen König vor dem Schach durch den Läufer geschützt hat, vom Brett verschwunden sein.
Das bedeutet aber, dass es sich nicht um eine schwarze Figur gehandelt haben kann, denn diese würde noch auf b6 stehen, denn Schwarz muss, davon haben wir uns schon überzeugt, zuletzt mit seinem König gezogen haben.
Nun gut: Auf b6 muss somit eine weiße Figur gestanden haben. Sie steht jetzt nicht mehr dort. Sie muss also, als der schwarze König nach a8 zog, verschwunden sein. Das bedeutet zwingend, dass sie auf a8 vom schwarzen König geschlagen worden sein muss.
Aber wie ist sie nach a8 gekommen? Sie muss beim Zug zuvor dorthin gezogen sein. Und zwar von b6. Aha: Es kann sich bei dieser Figur also nur um einen weißen Springer gehandelt haben. Damit haben wir die unmittelbare Vergangenheit mit zwingender Logik rekonstruiert: Vor je einem Zug von Schwarz und Weiß vor der Diagrammposition stand der schwarze König auf a7 und ein weißer Springer stand auf b6. Dieser Springer zog nach a8, worauf der schwarze König seitens des Läufers auf g1 im Schach steht. Dann schlägt der schwarze König den weißen Springer auf a8, was zur obigen Stellung führt.
Ihr Schachrätsel für Zuhause
Haben Sie Lust sich selbst einmal als Detektiv zu versuchen? Hier ist Ihre Chance. Die Problemstellung lautet: Schwarz ist am Zug. Kann er jetzt rochieren?
Math up your life!: Alle Folgen des Mathe-Blogs finden Sie hier.
