In letzter Zeit war viel von Steuerhinterziehung die Rede, meist im Zusammenhang mit Uli Hoeneß. Der hat nachweislich Millionen-Gewinne in seinen Steuererklärungen unterschlagen. Heraus kam das durch Recherchen von Journalisten und der schiefgegangenen Selbstanzeige des Fußball-Managers.
Andere Steuersünder sind da vermeintlich geschickter. Sie fälschen und manipulieren ihre Steuererklärungen gezielt, um die Finanzbeamten zu täuschen. Hier kommt die Mathematik ins Spiel – Fahnder nutzen sie sogar, um Steuersündern auf die Schliche zu kommen. Denn es gibt erstaunliche statistische Gesetzmäßigkeiten. Wenn die nicht erfüllt sind, schöpfen Steuerexperten Verdacht.
Aber der Reihe nach.
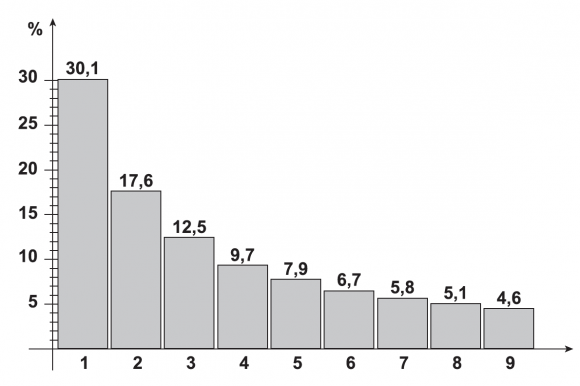
Es gibt mehr kleine als große Dinge in der Welt. Und auch in der Welt der Zahlen ist das so. Unser Kosmos hat wohl eine Vorliebe für Zahlen mit kleinen Anfangsziffern. Jede Zahl kann man schreiben, indem man einen Wert M zwischen 1 und 10 mit einer Zehnerpotenz multipliziert. Also 3,1 mal 10 hoch 2 statt 310. Kurioserweise treten in der Welt häufig Zahlen auf, deren Faktoren M kleiner als 4 sind. Das sind Zahlen mit Anfangsziffern 1, 2 oder 3.
Das können Sie feststellen, indem Sie eine beliebige Zeitungsseite aufschlagen oder eine Website aufrufen und die Anfangsziffern aller in den Artikeln auftretenden Zahlen oder Zahlwörter notieren. Solche mit kleinen Anfangsziffern bilden die Mehrheit. Genauer: Die Anfangsziffern der Zahlen vieler Datensätze – von Einwohnerzahlen über Naturkonstanten bis hin zu beliebig zusammen gemischten Werten in Nachrichten und Berichten – folgen der Benford-Verteilung, auch Benfordsches Gesetz genannt.
Der Abbildung ist zu entnehmen, dass die relative Häufigkeit der Anfangsziffer 1 mehr als 6 Mal größer ist als die der Anfangsziffer 9.
Für die meisten Menschen kommt das sehr überraschend. Es ist kein Grund erkennbar, warum unsere Welt zum Beispiel die Zahl 1.362 gegenüber der Zahl 9.362 favorisieren sollte. Sie unterscheiden sich nur um eine Ziffer. Und dennoch ist es so: Eine Zählung in einigen willkürlich gesuchten Google-Ergebnissen bestätigt Ihnen das sofort.
Wie kommt es zur Benford-Verteilung?
Wenn es ein allgemeingültiges Verteilungsgesetz der Anfangsziffern gibt, dann kann es nicht davon abhängen, in welchen Einheiten die Zahlen angegeben werden, ob in Celsius oder Fahrenheit, Kilometern oder Meilen, Euro oder Dollar. Das Gesetz muss auf jeder infrage kommenden Mess-Skala gelten, also universell sein. Mathematiker nennen diese Eigenschaft Skaleninvarianz.
Und Skaleninvarianz bedeutet etwas weitergedacht, dass die 10er-Logarithmen der obigen Faktoren M gleichmäßig im Intervall von 0 bis 1 variieren. Diese Gleichverteilung bei den Faktoren M führt dann zur Ungleichverteilung der Anfangsziffern gemäß Benford: Die Wahrscheinlichkeiten für die Anfangsziffern d = 1, 2, …, 9 betragen jeweils log(d + 1) – log(d).
Dieses Verteilungsgesetz gilt auch für die überwiegende Mehrheit von Finanzdaten: Echte, unverfälschte, saubere Finanzdaten folgen der Benford-Verteilung, fabrizierte Daten weichen davon ab.
Der US-Statistiker Mark Nigrini, Professor für Buchhaltungswesen, hat Daten über die Zinserträge, die amerikanische Banken an die Steuerbehörde leiten, statistisch untersucht und fand das Benford-Gesetz sehr genau erfüllt. Doch die von den Steuerpflichtigen in ihren Steuerklärungen angegebenen Beträge wichen oft davon ab.
Nigrini hat eine Software entwickelt, die bereits in vielen Ländern, auch in Deutschland, von Behörden und Wirtschaftsprüfern zum Aufspüren von manipulierten Steuererklärungen und gefälschten Bilanzen eingesetzt wird. Er hat sie an Fällen zugegebener Steuerhinterziehung getestet: Keine der Erklärungen passierte seinen Benford-Test.
Es ist aber auch ziemlich schwierig, Daten so zu fälschen, dass sie weiterhin Benford-artig bleiben. Denn nicht nur die Anfangsziffern, sondern auch die folgenden Ziffern natürlich vorkommender Daten zeigen statistische Auffälligkeiten. Es mag nur ein kleiner Unterschied sein, wenn jemand einen tatsächlichen Gewinn von 16.432 Euro als 9.921 Euro nach unten drückt, doch schon diese eine Manipulation verzerrt das Gefüge der ersten beiden Ziffern erheblich. Und da es hier um die Ziffer „9“ geht, die einen starken Verzerrungshebel hat, kann der Datensatz schon dadurch auffällig werden. Etwas überpointiert könnte man sagen: Einen Daten-Guru kann man nicht belügen.
Wenn Steuererklärungen beim Benford-Test durchfallen, ist das natürlich kein juristisch zwingender Beweis für Fälschung, aber es ist ein Signal für die Steuerbeamten, einmal genauer hinzuschauen, Belege anzufordern, Einträge zu prüfen und eventuell eine Steuerrevision zu veranlassen. Wer denkt, das Finanzamt sei zu blöd, um Fälschungen aufzudecken, kann sich dabei leicht verrechnen.