Heute geht es um eine Multiplikationstechnik aus dem alten Arabien. Die moderne Bezeichnung dafür ist Gittermultiplikation. Sie ist zu verschiedenen Zeiten in verschiedenen Kulturen aufgetaucht. Doch zuerst findet sie sich beim marokkanischen Rechenmeister und Astronomen Ibn al Banna‘ al-Marrakushi (1256-1321).
Er übersetzte Euklids Elemente ins Arabische und schrieb selbst mehrere Dutzend Bücher. Sein berühmtestes ist Talkhis amal al-hisab (deutsch: Zusammenfassung der Rechenmethoden). Darin findet sich auch die folgende Methode.
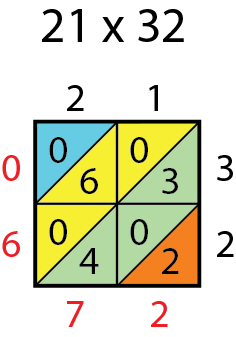
Betrachten wir das Produkt 21 x 32.
Abbildung von Vlad Sasu
Man arrangiert die Zahlen nach Art der Abbildung um ein Gitter herum, dessen Kästchen in der angegebenen Weise halbiert sind. Dann werden die Ziffern miteinander multipliziert, in jedes Kästchen kommt das Produkt der darüber und seitlich daneben stehenden Ziffern.
Die Produkte werden zweistellig in die Kästchen eingetragen, wobei die Zehnerstelle, eventuell 0, in der oberen Hälfte steht. Anschließend werden rechts beginnend die Ziffern in jeder Diagonalen addiert.
So geht Rechnen mit Leichtigkeit
In der Diagonalen ganz rechts steht nur die 2. In der Diagonalen daneben stehen die Ziffern 3, 0, 4. Deren Summe ist 7. Die nächste Diagonale enthält die Ziffern 0,6,0 mit Summe 6. In der verbleibenden Diagonalen steht nur eine 0. Diese Diagonalsummen bilden die Ziffern der Lösung: 672. So geht Rechnen mit Leichtigkeit.
Die Methode ist auch für mehrstellige Zahlen anwendbar.
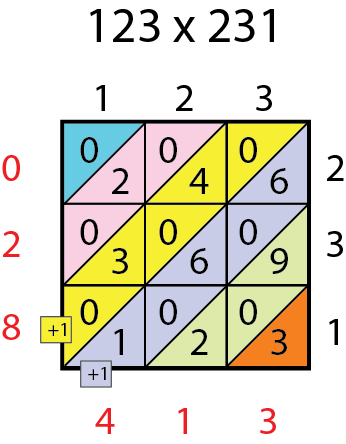
Ergibt sich bei der Summenbildung in den Diagonalen eine zweistellige Zahl, so wird nur deren Einerstelle als Ziffer der Lösung notiert und ihre Zehnerstelle zur Summe in der nächsten Diagonalen hinzuaddiert. Das sieht man am Beispiel 123 x 231.
Abbildung von Vlad Sasu
Also : 123 x 231 = 28413
Und hier wieder ein paar Vorschläge für den Selbstversuch:
365 x 42 =
123 x 456 =
33 x 44 =