Wenn wie jetzt wieder Millionen von Menschen vom Fußballfieber befallen sind, hat vermeintlich Abseitiges nur geringe Chancen aufzufallen. Umso glücklicher schätze ich mich, Ihre Aufmerksamkeit zu haben. Ohne längere Vorrede stelle ich Ihnen ein ungemein schönes, cooles und spektakulär ungewöhnliches Verfahren für schnelles Multiplizieren zweistelliger Zahlen vor. Es ist eine visuelle Methode und damit ein absolutes Must-See!
Die alten Chinesen haben sie erfunden, so wie sie auch schon das Papier, den Buchdruck und den Kompass lange vor den Europäern kannten.
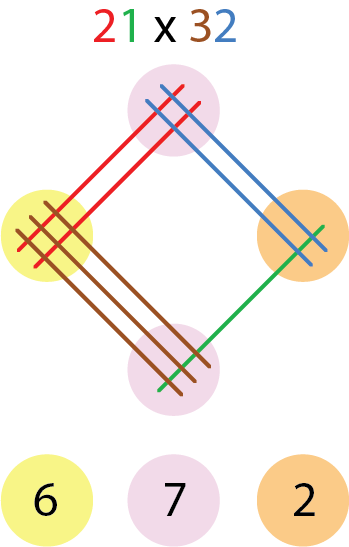
Beginnen wir mit 21 x 32.
Die Zehner- und Einerstellen werden in entsprechende Anzahlen von schräg angeordneten Linien übersetzt. Essstäbchen taten es damals auch schon.
Die folgende Abbildung zeigt dies durch Farbcodierung.
Abbildung: Vlad Sasu
Dann muss man nur noch die Schnittpunkte der Linien in den farblich markierten Bereichen abzählen. Fertig! Schneller als eine 5-Sekunden-Terrine.
Wie geht man vor, wenn in einem Bereich die Zahl der Schnittpunkte zweistellig ist?
Natürlich durch Zehnerübertrag in der naheliegenden Weise.
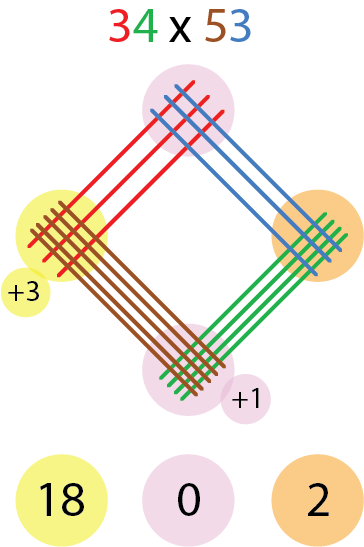
Nehmen wir 34 x 53.
Die folgende Abbildung ist ziemlich selbsterklärend.
Abbildung: Vlad Sasu
Also: 34 x 53 = 1802
Und nun viel Spaß beim Ausprobieren!
Hier einige Vorschläge:
13 x 14 =
53 x 32 =
44 x 26 =