Die Schach-Weltmeisterschaft in Sotchi ist Geschichte. Magnus Carlsen bleibt das Maß aller Dinge in der Kunst, Schach zu Spielen. Doch der harte Wettkampf zwischen zwei Spielern am Schachbrett ist nicht das einzig interessante am königlichen Spiel: Es hat vielfältige Beziehungen zu den Wissenschaften wie zum Beispiel zu Philosophie, Psychologie und nicht zuletzt zur Mathematik.
Etwa zu Pythagoras.
Denkt man an Pythagoras, fällt einem natürlich sein berühmter Satz ein: a2 + b2 = c2. Und schon ist man mitten im Thema der Geometrie. Für den Satz des Pythagoras gibt es mehr Beweise, als für jeden anderen mathematischen Satz. Einer dieser Beweise stammt sogar vom 20. US-Präsidenten James Garfield (1831-1881).
Heute soll in diesem Blog aber ein Schachbrett-Beweis des Satzes demonstriert werden. Denn anhand dessen können wir gleich mal über die kuriose Geometrie des Schachbretts sprechen.
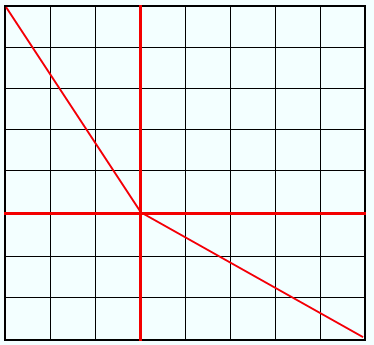
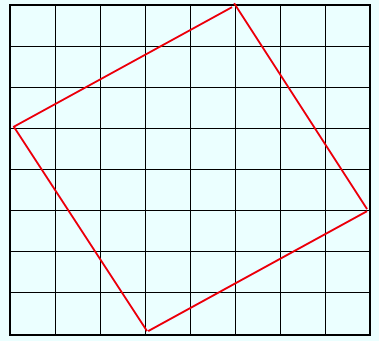
Für den Beweis reicht es, ein paar farbige Linien auf ein Schachbrett zu zeichnen. Und zwar auf zwei verschiedene Arten, so wie in den nächsten beiden Diagrammen abgebildet.
In beiden Abbildungen tauchen jeweils vier rechtwinklige Dreiecke auf. Eigentlich ist es immer ein und dasselbe Dreieck, aber es ist an vier Stellen auf dem Schachbrett platziert, dessen Schwarz-Weiß-Musterung der Felder wir der Übersicht wegen weggelassen haben.
Bezeichnen wir mit c die Länge der längsten Dreiecksseite und mit a, b die Längen der beiden kürzeren Seiten. Dem ersten Diagramm ist zu entnehmen, dass die Fläche des Schachbretts, welche die vier Dreiecke nicht abdecken, also die Fläche der beiden Quadrate, sich so berechnen lässt: a2 + b2.
Im unteren Diagramm sind dieselben vier Dreiecke anders positioniert. Die Fläche des Schachbretts, die sie nicht abdecken, ist die Fläche des großen Quadrates in der Mitte. Diese Fläche ist c2. Dieses Quadrat ist also genauso groß wie die beiden kleinen Quadrate im ersten Diagramm. Und fertig ist der Schachbrett-Beweis des Satzes von Pythagoras für das gegebene, aber beliebige rechtwinklige Dreieck.
Insofern hat Pythagoras recht auf dem Schachbrett.
Man könnte jetzt denken, dass die Geometrie des Schachbretts genau so ist, wie die Geometrie der Welt. Das stimmt aber nicht. Die Schach-Geometrie besitzt bemerkenswerte Besonderheiten.
Definiert man etwa den Abstand zwischen zwei Feldern auf dem Schachbrett als minimale Anzahl von Zügen, die der König benötigt, um von einem Feld zum anderen zu ziehen, so ist zum Beispiel der Abstand zwischen zwei diagonal gegenüber liegenden Eckfeldern (a1 und h8 oder a8 und h1, siehe unten für die Beschriftung der Reihen und Spalten des Schachbretts) genauso groß wie der Abstand von Eckfeldern auf derselben Linie (a1 und h1 oder h1 und h8), nämlich in beiden Fällen sieben Königsschritte.
Trotzdem ist auf dem Schachbrett vieles anders
In unserer Alltagsgeometrie dagegen ist der Abstand längs der Diagonalen gemessen in Zentimetern um den Faktor Wurzel aus 2 größer. Es gibt kein einfacheres und gleichzeitig spektakuläreres Beispiel, um die Auswirkungen der besonderen Schach-Geometrie darzustellen, als das folgende berühmte Schachproblem, das vom ungarischen Großmeister Richard Reti 1921 komponiert wurde: Weiß zieht und hält Remis.
Der weiße König soll also diese Stellung, die so klar für Schwarz gewonnen aussieht, noch ins Unentschieden retten. Das ist nicht nur eine Höchstschwierigkeit, sondern verlangt scheinbar das Unmögliche. Warum?
Der schwarze König kann den weißen Bauern leicht von der Umwandlung in eine Dame hindern. Er steht ja nicht weit von ihm entfernt. Umgekehrt steht der weiße König aber weit vom schwarzen Bauern entfernt, der drei Felder Vorsprung hat für den Lauf nach h1, wo er sich in eine Dame umwandeln kann.
Wie also kann der weiße König auch nur daran denken, diese Stellung noch zu retten? Nicht einmal ein oder zwei Wunder scheinen dafür auszureichen.
Aber der Schein trügt. Die Rettung wird möglich durch die kuriose Geometrie des Schachbretts. Und zwar mit dem Manöver 1.Kg7 h4 2. Kf6 Kb6. Wenn an dieser Stelle Schwarz den Bauern nach h3 gezogen hätte, dann könnte der weiße König seinen eigenen Bauern schützen und ihm helfen, sich in eine Dame umzuwandeln. Das geht so: 3.Ke7 h2 4. c7 Kb7 5. Kd7 und mit den nächsten beiden Zügen von Schwarz und Weiß entstehen zwei Damen auf dem Brett, so dass die Stellung Remis ist.
Wenn aber Schwarz im zweiten Zug den König nach b6 zieht, geht es weiter mit 3.Ke5 K schlägt c6 (Alternativ führt der Zug des schwarzen Bauern nach h3 wegen 4.Kd6 h2 5.c7 Kb7 6.Kd6 wieder zur Entstehung zweier sich neutralisierender Damen.) Nachdem der schwarze König aber im dritten Zug den Bauern auf c6 geschlagen hat, sichert sich der weiße König das Unentschieden, indem er im Gegenzug den schwarzen Bauern niederstreckt mit 4.Kf4 h3 5.Kg3 h2 6.König schlägt h2 und Unentschieden. Die Quadratur des Quadrats ist geglückt!
Das rettende Manöver des weißen Königs basiert also darauf, dass er zwei Ziele gleichzeitig verfolgen kann. Einmal den Angriff auf den schwarzen Bauern und zum anderen die Unterstützung des eigenen Bauern bei der Umwandlung in eine Dame. Die gleichzeitige Verfolgung beider Ziele wird durch die Schachgeometrie ermöglicht. Der winkelförmige Umweg h8-g7-f6-e5-f4-g3-h2 ist nämlich genau so lang wie der direkte Weg h8-h7-h6-h5-h4-h3-h2. Das heißt: Die Summe der Längen der Schenkel im Dreieck mit den Ecken h8, e5, h2 ist gleich der Länge der Grundlinie h8-h2. Für beide benötigt der König genau sechs Schritte.
In unserer vertrauten Alltagsgeometrie ist der kürzeste Weg zwischen zwei Punkten die gerade Linie, die diese beiden Punkte miteinander verbindet. Jeder Weg, der wie auch immer von dieser Geraden abweicht, ist länger. In der Geometrie des Schach-Universums gibt es mehr als nur einen kürzesten Weg zwischen nicht benachbarten Feldern. Darunter kann auch ein Zick-Zack-Kurs sein oder ein dreieckiger oder bogenförmiger Pfad.
Haben Sie Lust, selbst einmal die Geometrie des Schachs zu erforschen? Dann können Sie das mit folgendem Schachproblem von Artur Mandler aus dem Jahr 1931 tun.
Weiß ist am Zug und soll gewinnen! Mit welcher Zugfolge kann er das schaffen?
Math up your life!: Alle Folgen des Mathe-Blogs finden Sie hier.