In der Adventszeit erstrahlt so manches Haus festlich. Doch für die schicke Weihnachtsbeleuchtung müssen alljährlich widerspenstige Lichterketten gezähmt werden. Egal wie sorgsam sie im Jahr zuvor verstaut wurden: Wer sie aus den Kisten hervorholt, findet sie heillos verknotet vor.
Wie gut, dass Sie in diesem Jahr das Mathe-Blog haben. Denn Knoten sind ein Fall für die Mathematik.
Es gibt sogar eine ganz ausgefeilte mathematische Knotentheorie. Sie hat enorm interessante Eigenschaften vom Krawatten- bis zum Seemannsknoten zu Tage gefördert.
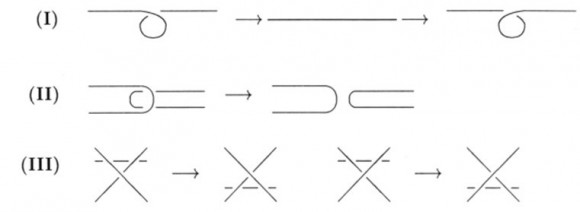
Zum Beispiel, dass ich jede geschlossene und entwirrbare Lichterkette – deren Schlaufen also nicht ineinander verschlungen sind – mit (eventuell mehrfacher Anwendung von) nur drei verschiedenen Manövern, den Reidemeister-Bewegungen, entwirren kann. Das sind die folgenden:
- (I) Man kann eine Schlaufe entfernen oder hinzufügen.
- (II) Man kann eine Kreuzung entfernen oder hinzufügen.
- (III) Man kann einen Strang des Knotens von einer Seite einer Kreuzung auf die andere legen.
Ins Schematische übersetzt sieht das dann so aus:
Abbildung : Reidemeister-Bewegungen
Das ist im Wesentlichen der Inhalt des Reidemeister-Theorems. Es geht zurück auf den deutschen Mathematiker Kurt Reidemeister (1893-1971), der es 1926 bewies. 1933 wurde er nach der Machtergreifung der Nationalsozialisten aus seinem Professorenamt entlassen.
Wenn also ein Knoten entknotet werden kann, dann kann man das mit nur drei Arten von Manövern tun.
Das Theorem bietet sich doch geradezu an für eine kleine Vorweihnachtsknobelei:
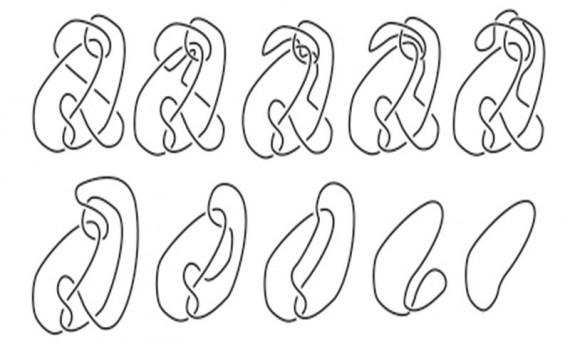
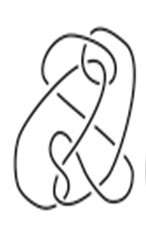
Ist die folgende Lichterkette – aus einer wissenschaftlichen Arbeit von Louis Kauffman und Sofia Lambropoulou – heillos verknotet, oder kann man sie zu einem geschlossenen Schnurring entwirren?
Hier ist die Antwort:
Man kann die Kette tatsächlich aufdröseln. Die folgende Abbildung zeigt die einzelnen Reidemeister-Manöver:
Wenn Sie es nicht glauben, können Sie den Knoten auch mit einem längeren Faden auf einem Tisch selbst auslegen, ihn dann aufnehmen und sehen wie er zu einem Ring wird.
Was sich mit der Knotentheorie noch anfangen lässt? Zum Beispiel das Universum erklären mit der String-Theorie, nach der unsere Welt nicht aus winzigen kugelförmigen Elementarteilchen in drei Dimensionen besteht, sondern aus noch winzigeren, teils geschlossenen, teils verknoteten Energie-Fäden (Strings) in zehn Dimensionen.
Die String-Theorie ist ein Produkt der großen Suche nach der Weltformel, der vereinheitlichten Theorie aller Elementarteilchen und aller ihrer Wechselwirkungen. Die Knotentheorie hilft, die komplexen Eigenschaften der Strings zu verstehen.
Nach Ansicht des Nobelpreisträgers David Gross von der University of California, Santa Barbara, an der ich das Glück hatte, mich in den letzten beiden Jahren zehn Monate zu Forschungszwecken aufzuhalten, ist die String-Theorie entweder selbst die Weltformel oder zumindest ein sehr wichtiger Schritt dorthin.
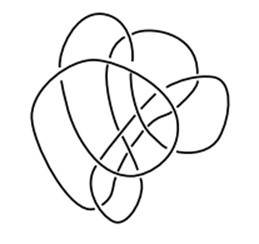
Zugabe: Sollte obiges Beispiel zu schwer sein, können Sie auch über folgendes Gewirr nachdenken, das praktisch mit bloßem Auge entwirrt werden kann.