Die Quadratur des Kreises ist ein Problem aus der Geometrie, das Jahrtausende alt ist. Die Aufgabe besteht darin, zu einem Kreis ein Quadrat mit exakt demselben Flächeninhalt zu konstruieren. Verlangt man, dass hierfür nur Zirkel und Lineal verwendet werden, ist diese Aufgabe nicht lösbar. Das hat im Jahr 1882 der Mathematiker Ferdinand von Lindemann bewiesen.
Wegen dieser Unmöglichkeit ist der Begriff Quadratur des Kreises in vielen Kulturen der Welt zum Sinnbild einer nicht ausführbaren Aufgabe geworden. Überschriften wie „Die Quadratur des Kreises mit der Schweiz“ oder „Kerry versucht sich in der Quadratur des Kreises“ sind nur einige der Überschriften aus der Presse der vergangenen Tage und Wochen.
Dabei ist die Quadratur des Kreises nicht generell unmöglich. Sehen Sie selbst:
Abbildung: Vlad Sasu
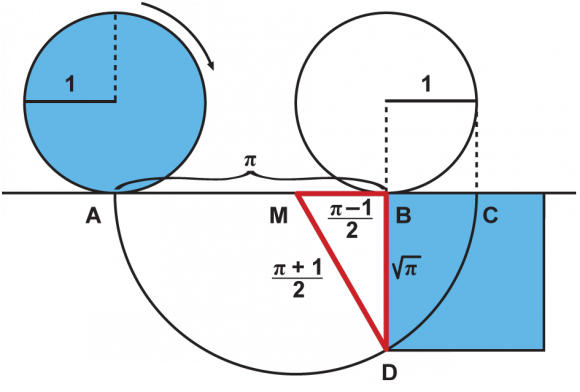
Der Kreis hat eine halbe Drehung ausgeführt. Die blau gezeichneten Flächen von Kreis und Quadrat sind jeweils gleich Pi. Das rechtwinklige rote Dreieck spielt hierbei eine wichtige Rolle. Mit dem Satz des Pythagoras lässt sich leicht prüfen, dass die zur Strecke von M nach B senkrechte Dreiecksseite eine Länge von genau der Wurzel aus Pi hat. Damit ist der Kreis erfolgreich in ein Quadrat gleicher Fläche umgewandelt.
Als Ergebnis können wir festhalten: Mit Zirkel und Lineal geht die Quadratur nicht. Aber wenn ich zusätzlich eine Drehbank hinzunehmen darf, um den Kreis halb abzurollen, dann ist es möglich.