Am 13. August 1961 begann der Bau der Berliner Mauer. Acht Jahre später besuchte der amerikanischer Mathematiker und Physiker Richard J. Gott die Grenze – und fragte sich, wie lange die Mauer wohl noch stehen werde. Statt den weiteren Verlauf komplizierter weltpolitischer Ereignisse zu prognostizieren und daraus eine Vorhersage abzuleiten, fasste er den Entschluss, stochastisch zu argumentieren.
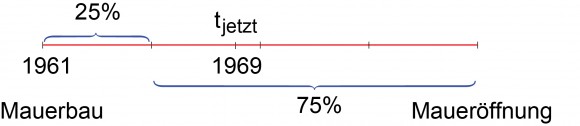
Da Gott (Richard J.) sich gegenüber der Gesamtexistenzdauer der Mauer als rein zufälligen Besucher wähnte, konnte er mit 75 prozentiger Gewissheit sagen, dass der zufällige Zeitpunkt tjetzt seines Mauerbesuchs nach dem ersten Viertel der Gesamtexistenzdauer der Mauer passierte. Damit lag sein Besuch im zeitlichen Bereich der letzten drei Viertel von deren Existenz. Befindet sich tjetzt am linken Rand des 75-Prozent-Bereiches, ist die Zukunft der Mauer am längsten, nämlich dreimal so lang wie die bisherige Vergangenheit von acht Jahren. Richard Gott konnte also damals zu 75 Prozent sicher sein, dass die Mauer 3 x 8 = 24 Jahre später, also 1993, nicht mehr stehen würde. Und sie fiel ja auch 1989.
Abbildung von Vlad Sasu: Grundüberlegung zu Richard Gotts Prognosemethode
Dies ist eine simple, aber dennoch in ihrer Einfachheit geniale stochastische Methode, die zukünftige Dauer eines beliebigen Phänomens mit gewünschter Sicherheit allein (!) unter Verwendung von dessen bisheriger Existenzdauer zu prognostizieren. Das geht auch für die weitere Publikationsdauer Ihrer Lieblingszeitschrift bis zum Publikationsende oder gar den weiteren Fortbestand der Menschheit bis zum Aussterben.
Die Methode ist absolut minimalistisch und benötigt nur einen als rein zufällig interpretierbaren Zeitpunkt im gesamten Existenzintervall des untersuchten Phänomens. Das aber ist essentiell. Die Gültigkeit der Methode steht und fällt mit der Verfügbarkeit eines solchen rein zufälligen Zeitpunktes. Wird man etwa kurz nach der Hochzeit eines Paares zu dessen erster Party als Ehepaar eingeladen, ist es nicht berechtigt, diesen Zeitpunkt zur Prognose der Länge der Ehe zu verwenden.
Alltagsprognosen leicht gemacht
Gotts Methode ist aber zum Beispiel in der folgenden Situation anwendbar: Sie besuchen China und werden von einem chinesischen Freund zu einem Sportereignis eingeladen. Sie wissen nichts über das Ereignis und fragen sich, wie viele Zuschauer wohl kommen werden. Sie schauen auf Ihrem Ticket nach und sehen, dass es sich um die Ticketnummer 37 handelt. Wie kann man eine Aussage über die Anzahl der Zuschauer treffen?
Mit einer Wahrscheinlichkeit von 50% gehört Ihre Ticketnummer 37 zur zweiten Hälfte der insgesamt verkauften Tickets. Also werden mit einer Wahrscheinlichkeit von 50 Prozent höchstens 73 Menschen zu der Veranstaltung kommen. Denn wenn 74 oder noch mehr Tickets verkauft worden wären, dann läge die Ticketnummer 37 in der ersten Hälfte verkaufter Tickets.
Will man mehr Sicherheit, so lässt sich die Vertrauenswahrscheinlichkeit auf 80, 90, 95 Prozent oder noch größere Wahrscheinlichkeiten erhöhen. Ist man etwa mit 90 Prozent zufrieden, sollte man zunächst überlegen, dass mit einer Wahrscheinlichkeit von 10 Prozent Ihre Ticketnummer zum ersten Zehntel der Menge aller verkauften Tickets gehört – das erste Zehntel umfasst also mit einer Wahrscheinlichkeit von 10 Prozent mindestens 37 Tickets. Mit 10-prozentiger Wahrscheinlichkeit wurden also mindestens 10 x 37 = 370 Tickets verkauft und mit der zugehörigen Gegenwahrscheinlichkeit von 90 Prozent weniger als 370 Tickets. Sie können somit ziemlich sicher sein, dass Ihr Freund Sie nicht zu einer Großveranstaltung eingeladen hat.
Jetzt sind Sie an der Reihe: Jemand liest Ihnen seinen Lieblingsabsatz aus einem Buch vor und erwähnt, dass er auf Seite 27 steht. Wie schätzen Sie die Gesamtseitenzahl des Buches mit einer Vertrauenswahrscheinlichkeit von 95 Prozent?