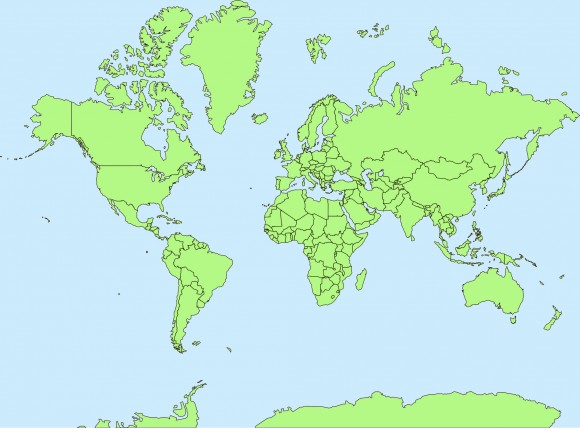
Grönland hat eine Gesamtfläche von etwa 2,17 Millionen Quadratkilometern. Der gesamte Kontinent Afrika ist fast 14 Mal so groß. Auf dem Papier. Auf Weltkarten wie der am Anfang dieses Textes wirkt Grönland dennoch viel größer, als es im Verhältnis zu anderen Ländern ist. Ein Scheinriese quasi, wie der freundliche Herr Tur Tur aus Michael Endes Buch Jim Knopf und Lukas der Lokomotivführer, der immer kleiner wird, je näher man ihm kommt. Doch woran liegt das?
Zunächst einmal daran, dass sich unsere dreidimensionale Erde relativ schlecht auf einem Blatt Papier abbilden lässt. Deshalb gibt es keine ideale Karte. Keine zweidimensionale Darstellung der Weltkugel kann gleichzeitig Verhältnisse von Winkeln, Flächengrößen und Längen realitätsgetreu darstellen. Daher kennt die Kartographie verschiedene Darstellungsmodelle. Die Washington Post führt in dieser Grafik einige davon auf und zeigt, wie sich – je nach Art der Projektion – das Größenverhältnis von Afrika und Grönland (grün eingefärbt) ändert.
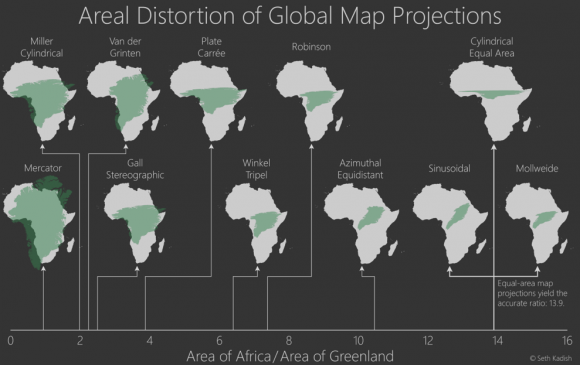
Und damit sind wir wieder bei der Karte am Anfang dieses Textes. Sie ist eine Mercator-Projektion (in der Washington-Post-Grafik links unten zu finden) – eine winkeltreue Darstellung der Erdkugel, die jedoch dazu führt, dass Flächengrößen nicht immer im korrekten Verhältnis angezeigt werden. Das ist auch die Erklärung, warum Grönland auf diesen Karten so groß ist.
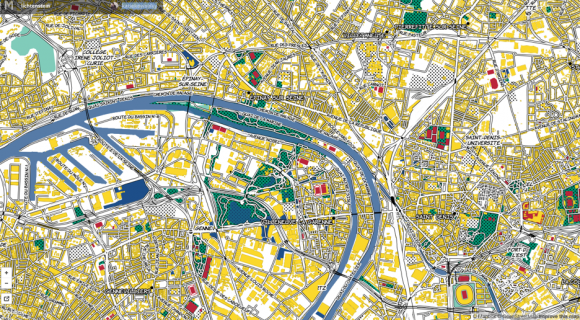
Im Netz verbreitet sich derzeit übrigens noch eine weitere Kartensammlung – und da ist die Art der Darstellung zunächst nicht entscheidend. Bei Katie Kowalsky, die Stadtpläne in Pop Art à la Roy Lichtenstein umgewandelt hat, geht es vor allem um Ästhetik.
Weitere Teilchen finden Sie hier.