Ein Algorithmus ist eigentlich eine mathematische Anleitung, um etwas auszurechnen. Manche Mathematiker sehen das mit dem Ausrechnen aber nicht so eng: Für sie sind Algorithmen regelrechte Mathe-Bastelanleitungen, für Rechenergebnisse oder andere Objekte aus der Mathematik. Da liegt es nahe, an Handwerk zu denken, an den Bau von Möbeln – und an Ikea-Bauanleitungen für Pax, Billy oder Metod.
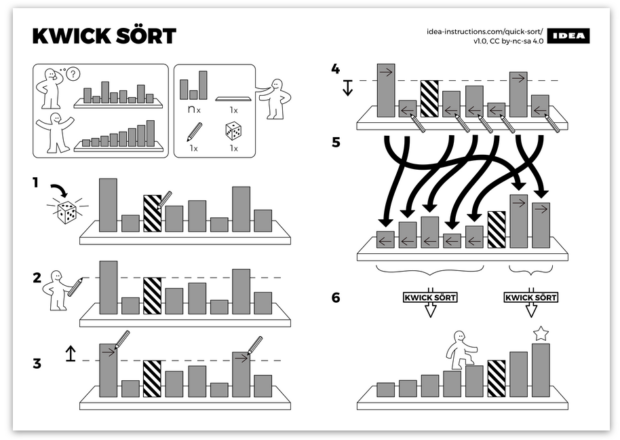
Sebastian Morr und Sándor P. Fekete sind offenbar genau solche Mathe-Bastler. Fekete ist Professor an der TU Braunschweig, Morr freischaffender Informatiker und ehemaliger Student Feketes. Zu zweit hatten sie die Idee, einige mathematische Algorithmen in die Bildersprache von Ikea-Bauanleitungen zu übersetzen. Das Ganze nennt sich dann IDEA. So entstanden Anleitungen zu „Kwick Sört“ oder „Merge Sört“, Sortieralgorithmen, die Fachleute bisher als „Quicksort“ und „Merge Sort“ kannten.
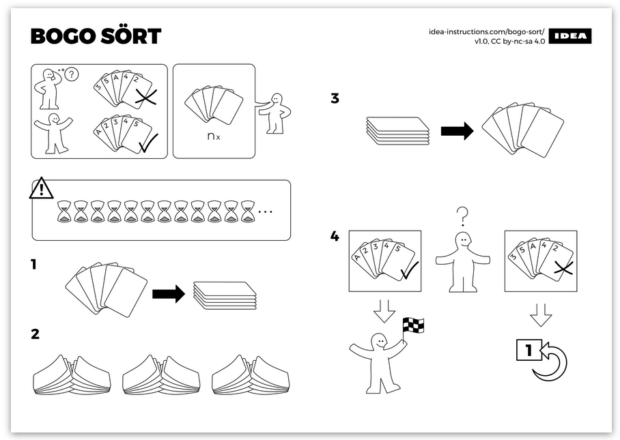
Es gibt aber auch eine Anleitung zu „Bogo Sört“, einem ziemlich dämlichen Sortieralgorithmus: Um damit ein Set Spielkarten zu sortieren, mischt man bei „Bogo Sört“ einfach so lange, bis die Karten zufällig in der richtigen Reihenfolge sind. Mathematisch gesehen ist das ein Algorithmus, praktisch ist es nicht. Daher wird der Anleitung eine Warnung mit zwölf Sanduhren vorangestellt. Die Algorithmiker der TU Braunschweig erklären aber auch, wie die Public-Key-Verschlüsselung funktioniert („Public Key Krüpto“) oder wie man das Haus vom Nikolaus und andere „Graphen“ in einem Strich zeichnen kann („One Ströke Dråw“).
„Wir wollen zeigen, dass Algorithmen mehr als Textzeilen sind – oder irgendwelche geheimnisvolle Dinge, die unser Leben bestimmen“, sagt Sándor Fekete über das Projekt. Doch nicht immer ist es einfach, die Bildsprache zu entschlüsseln. Wer „One Ströke Dråw“ wirklich verstehen will, braucht ohne Vorwissen vermutlich länger als für den Zusammenbau eines Pax-Kleiderschranks. Das liegt auch daran, dass mathematische Algorithmen eben doch mehr sind als Ikea-Anleitungen: Bei Ikea ist der „Input“ exakt bis zur letzten Schraube vorgegeben, mathematische Algorithmen kann man dagegen immer auf viele verschiedene mögliche Eingabeszenarien anwenden. Das macht sie kompliziert. Immerhin kommt man ohne IKEA-Imbusschlüssel aus.