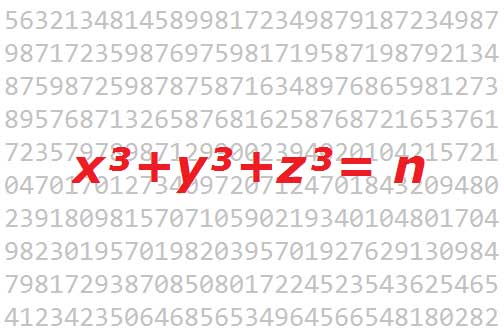
Mathematik ist nicht nur ein Kunstwerk, an dem gleichzeitig Hunderttausende Menschen arbeiten, sie ist auch ziemlich alt. Eine ganze Menge aktueller Aufgaben wurde schon in der Antike angedacht. Ein Beispiel: diophantische Gleichungen, benannt nach dem antiken Mathematiker Diophantos von Alexandria. Der knobelte an solchen Aufgaben: Gesucht werden zwei ganze Zahlen. Verdoppelt man die erste und verdreifacht die zweite und addiert alles zusammen, dann kommt 18 heraus. Wie heißen die beiden Zahlen? Der Teufel steckt dabei im Detail „ganze Zahl“: Diophantos erlaubte sich für die Lösung nur Werte wie 1, 2, 3 oder -6, aber keine Brüche.
Diese ganzen Zahlen machen die ganze Schwierigkeit der Gleichungen aus, und auf ihnen beruht auch ein Teil ihrer Popularität in der Moderne. Denn viele Probleme der Gegenwart handeln von unteilbaren Dingen, die sich eben nur mit ganzen Zahlen beschreiben lassen. Da will man größte Anzahl Container berechnen, die auf einen Containerfrachter passen – und steckt, zack, knietief in diophantischen Gleichungen. Solche Gleichungen können unlösbar sein oder nur ein paar oder sogar unendlich viele Lösungen haben. Der Satz von Andrew Wiles, der in den Neunzigerjahren Pierre de Fermats Vermutung beantwortete, handelt im Kern von der Unlösbarkeit diophantischer Gleichungen: Fermat hatte 350 Jahre zuvor vermutet, dass es keine drei ganzen Zahlen x, y und z über null gibt, die die Gleichung x^3 + y^3 = z^3 erfüllen, wobei statt der 3 jede beliebige Potenz größer als 2 eingesetzt werden darf.
Ändert man Fermats diophantische Gleichung nur ein bisschen ab, entstehen sofort neue, oft ungelöste Fragen. Zum Beispiel die: Gibt es vier ganze Zahlen – also auch negative – x, y, z und c, die die Gleichung x^3 + y^3 + z^3 = c erfüllen? Klar ist: Das hängt vom Wert von c ab. Manchmal klappt es, zum Beispiel, wenn c die Zahl 34 ist. Dann nimmt man für x, y und z einfach die Zahlen -1, 2 und 3 und erhält: (−1)^3 + 2^3 + (3)^3 = −1 + 8 + 27 = 34. Bei anderen Werten von c klappt es aber auch nicht. Und bei insgesamt 14 Werten von c zwischen 1 und 1.000 wusste man bis vor Kurzem gar nicht, ob es funktioniert.
Im Blog der Deutschen Mathematiker-Vereinigung wird nun erzählt, dass der Mathematiker Andrew Booker von der University of Bristol mithilfe trickreicher Vereinfachungen herausgefunden hat: Auch 33 und 42 lassen sich zerlegen. Und übrigens: Die nächsten ungelösten Werte für c sind 74, 114, 165 …
Nachtrag nach einem Leserkommentar: Die Frage für auch c=74 bereits gelöst. 114 ist der derzeit kleinste ungelöste Fall.